前言

nlp-paper：NLP相关Paper笔记和代码复现
nlp-dialogue：一个开源的全流程对话系统，更新中！
说明：讲解时会对相关文章资料进行思想、结构、优缺点，内容进行提炼和记录，相关引用会标明出处，引用之处如有侵权，烦请告知删除。
转载请注明：DengBoCong

为何在获取输入词向量之后需要对矩阵乘以embeddding size的开方？

1
2
3
embeddings = tf.keras.layers.Embedding(input_dim=vocab_size, output_dim=embedding_dim,
                                           dtype=d_type, name="{}_embeddings".format(name))(inputs)
embeddings *= tf.math.sqrt(x=tf.cast(x=embedding_dim, dtype=d_type), name="{}_sqrt".format(name))

我上面使用的是Keras的Embedding，其初始化方式是xavier init，而这种方式的方差是1/embedding size，因此乘以embedding size的开方使得embedding matrix的方差是1，在这个scale下可能更有利于embedding matrix的收敛。

Transformer为何使用多头注意力机制？

先上一份原论文中对Multi-head attention的解释：

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.

  • 如何解释这个不同的注意力表示子空间？
  • 以及表示子空间信息的差异性是如何来的？

对于这两个小问题，我从这个回答中找到了思路：为什么Transformer 需要进行 Multi-head Attention？。

首先，有大量的paper表明，Transformer或Bert的特定层是有独特的功能的，底层更偏向于关注语法，顶层更偏向于关注语义，其实这也符合我们的直觉（语法与token位置相关性较大，语义则是更高层的抽象表示）。这反应了结构中不同层所学习的表示空间不同，从某种程度上，又可以理解为在同一层Transformer关注的方面是相同的，那么对该方面而言，不同的头关注点应该也是一样的，而对于这里的“一样”，一种解释是关注的pattern相同，但内容不同，这也就是解释了第一个小问题，不同的头大体上的pattern是一样的，而差异性来源与分离的不同内容，为了更好的说明这一点，从论文：A Multiscale Visualization of Attention in the Transformer Model中截取的一张可视化的图可以形象的说明：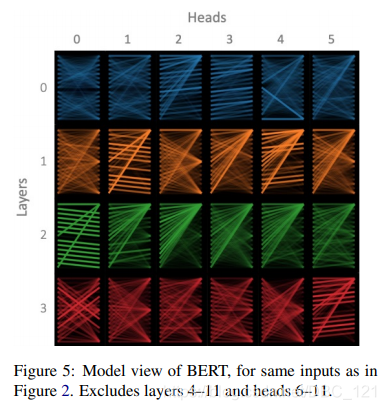
在这里插入图片描述
可以看到，相同层的不同头所关注的pattern大致相同，不过细心的小伙伴应该会注意到，同一层中总是有那么一两个头和其他头的pattern不相同，这也是所要解释的第二个小问题。

我们首先来看看这个过程是怎样的。首先，所有的参数随机初始化，然后用相同的方法前传，在输出端得到相同的损失，用相同的方法后传，更新参数。在这一条逻辑线中，唯一不同的地方在于初始值的不同。设想一下，如果我们把同一层的所有参数（这里的参数都是指的$W^Q_i,W^K_i,W^V_i$ ）初始化成一样的（不同层可以不同），那么在收敛的时候，同一层的所有参数仍然是一样的，自然它们的关注模式也一样。也就是说，相同层中出现的“异类”，从某种解释上说，可以理解为是由于初始化的不一样引起的。

我还看到了另外一种从实用原因解释的思路，来自苏剑林大神的回答，总体上表述的意思是，每个token通常只是注意到有限的若干个token，这说明Attention矩阵通常来说是很“稀疏”的，所以只用一个头的话，当特征维度较大时，计算量就大，这个时候用某种方式对 $Q,K$ 进行分割，然后计算之后在以某种方式整合，虽然这种方式计算量和不分割差不多，但是从某种程度上引入了enhance或noise，类似模型融合，效果表现上也应该更好。

最后总结陈词就是，Multi-Head其实不是必须的，去掉一些头效果依然有不错的效果（而且效果下降可能是因为参数量下降），这是因为在头足够的情况下，这些头已经能够有关注位置信息、关注语法信息、关注罕见词的能力了，再多一些头，无非是一种enhance或noise而已。

计算Attention时，点乘Attention和加法Attention的区别？

Attention发展到现在衍生出了特别多的种类，从功能效果上来说，Attention可以分为基于内容的注意力机制(content-based attention)、基于位置的注意力机制(location-based attention)和混合注意力机制(hybrid attention)，我之前针对Attention做了一个总结，感兴趣的小伙伴可以看一下：NLP中遇到的各类Attention结构汇总以及代码复现。
$$score(h_j,s_i)=\left \langle v,tanh(W_1h_j+W_2s_i) \right \rangle$$ $$score(h_j,s_i)=\left \langle W_1h_j,W_2s_i \right \rangle$$

而我们这里讨论的点乘Attention和加法Attention属于基于内容的注意力机制(content-based attention)，我们从计算速度上和效果上来比较它们两者间的区别。

  • 从计算效率上，为了方便感官上的呈现，看下面的两者计算注意力分数的代码，从这里其实很容易看得出来，整体计算量上，它们两者是相似的，在GPU运行上应该没有很明显的差别。
    1
    2
    加法：score = self.V(tf.nn.tanh(self.W1(key) + self.W2(tf.expand_dims(query, 1))))
    点乘：score = tf.matmul(query, key, transpose_b=True) / tf.math.sqrt(dk)
  • 从表现效果来讲，论文：Massive Exploration of Neural Machine Translation Architectures里面对此做了对比实验（这篇Paper里基于Seq2Seq做了许多对比实验，很值得阅读，也可以阅读我之前的论文阅读笔记：对NMT架构的超参数首次进行大规模消融实验分析），Paper的实验结果如下：
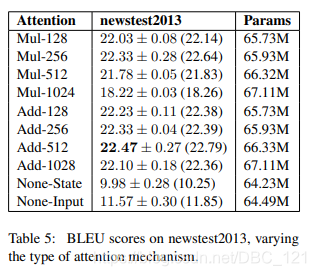
    在这里插入图片描述
    从结果上可以看得出，加法式注意机制略微但始终优于乘法式注意力机制。当然优于Transformer结构中使用了的多头注意力机制，在将表示分割成不同个头进行运算时，使用点乘会更加灵活方便计算，但实际应用在Transformer上的差别，后面实验对比再体会体会。

    transformer中为什么使用不同的K 和 Q？

  • 问题

我们来看看原论文中的公式：
$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
这就是我们非常熟悉的Self-Attention的计算公式，在这里Q和K是相同的，但是在真正的应用中，通常会分别给K和Q乘上参数矩阵，这样公式会变成如下这样（其中两个参数矩阵进行共享的话，就是reformer的做法）：
$$Attention(Q,K,V)=softmax(\frac{Q(W_qW^T_k)K^T}{\sqrt{d_k}})V$$
在这里，我们把目光放在Softmax上，当Q和K乘上不同的参数矩阵时，根据softmax函数的性质，在给定一组数组成的向量，Softmax先将这组数的差距拉大（由于exp函数），然后归一化，它实质做的是一个soft版本的argmax操作，得到的向量接近一个one-hot向量（接近程度根据这组数的数量级有所不同）。这样做保证在不同空间进行投影，增强了表达能力，提高了泛化能力。

如果令Q和K相同，那么得到的模型大概率会得到一个类似单位矩阵的attention矩阵，这样self-attention就退化成一个point-wise线性映射，对于注意力上的表现力不够强。

Transformer中的Attention为什么scaled?

在上一个问题中，我们有提到计算Attention分数时，是通过Softmax进行归一化的，而Softmax有可以当作argmax的一种平滑近似，与argmax操作中暴力地选出一个最大值（产生一个one-hot向量）不同，softmax将这种输出作了一定的平滑，即将one-hot输出中最大值对应的1按输入元素值的大小分配给其他位置。而当喂入的数组内部数量级相差较大时，“1分出去的部分”就会越来越少，当数量级相差到一定程度，softmax将几乎全部的概率分布都分配给了最大值对应的标签，其效果也就被削减了。不仅如此，在输入的数量级很大时，还会导致softmax的梯度消失为0，造成参数更新困难，这也是为什么需要对输入先进行缩放的原因。

其次，为什么原文中的计算公式对输入缩放的大小是 $\sqrt{d_k}$？原论文中是这样解释的：

To illustrate why the dot products get large, assume that the components of q and k are independent random variables with mean 0 and variance 1. Then their dot product, $q\cdot k=\sum^{d_k}_{i=1}q_ik_i$, has mean 0 and variance dk.

假设向量 $q$ 和 $k$ 的各个分量是互相独立的随机变量，均值是0，方差是1，那么点积 $q\cdot k$ 的均值是0，方差是 $d_k$ 。而方差越大也就说明，点积的数量级越大（以越大的概率取大值）。那么一个自然的做法就是将点积除以 $\sqrt{d_k}$ ，将方差控制为1，也就有效地控制了前面提到的梯度消失的问题。

在计算注意力分数的时候如何对padding做mask操作？

mask是将一些不要用的值掩盖掉，使其不产生作用，有两种mask，第一种是padding mask，在所有scaled dot-product attention都用到，第二种是sequence mask，在decoder的self-attention里面用到。

  • padding mask：因为一个批量输入中，所有序列的长度是不同的，为了符合模型的输入方式，会用padding的方式来填充（比如填0），使所有序列的长度一致。但填充部分是没有意义的，所以在计算注意力的时候，不需要也不应该有注意力分配到这些填充的值上面。所以解决方式就是在填充的位置赋予一个很小的负值/负无穷（-np.inf）的值，经过softmax后的得分为0，即没有注意力分配到这个上面。
1
seq = tf.cast(x=tf.math.equal(seq, 0), dtype=tf.float32)[:, tf.newaxis, tf.newaxis, :]
  • look_ahead_mask：我们知道在计算Q和K的时候，我们目的是通过self-attention获得某个token和它相关联token之间的关联程度，即我们Q和K相乘时，得到一个shape的最后两维为(…seq_len,seq_len)的相关性矩阵，但是，在我们将这个相关性矩阵送进Softmax进行计算之前，我们需要为了防止穿越mask所计算的那个token之后的其他token，为了更方便理解，可以看下面的图：
    在这里插入图片描述

    为什么 Transformer 需要 positional encoding ？

  • https://www.zhihu.com/question/347678607/answer/835053468

在没有 Position embedding 的 Transformer 模型并不能捕捉序列的顺序，交换单词位置后 attention map 的对应位置数值也会进行交换，并不会产生数值变化，即没有词序信息。所以这时候想要将词序信息加入到模型中。

Transformer 使用的解决方案是三角函数实现相对位置信息的表示。原回答已经对论文中的公式做了细致的解释，实质上就是对不同维度使用不同频率的正/余弦公式进而生成不同位置的高维位置向量。不过这里有一点需要解释，为什么奇偶维度之间需要作出区分，分别使用 sin 和 cos 呢？个人觉得主要是因为三角函数的积化和差公式。不过也正如tensor2tensor 的作者对其简洁版本公式的解释那样，奇偶区分可以通过全连接层帮助重排坐标，所以可以直接简单地分为两段(前 256 维使用 sin，后 256 维使用 cos)。

那么我们如何加入到模型中去呢？fairseq 和 Transformer 都是直接把词向量和位置向量直接相加的方式，让人感到疑惑的是为什么不进行拼接？

[W1 W2][e; p] = W1e + W2p，W(e+p)=We+Wp，就是说求和相当于拼接的两个权重矩阵共享(W1=W2=W)，所以拼接总是不会比相加差的。但是由于参数量的增加，其学习难度也会进一步上升。

无论拼接还是相加，最终都要经过多头注意力的各个头入口处的线性变换，进行特征重新组合与降维，其实每一维都变成了之前所有维向量的线性组合。所以这个决定看上去是根据效果决定的，参数少效果好的相加自然成了模型的选择。

transformer 为什么使用 layer normalization，而不是其他的归一化方法？

回答中有一个观点我觉得挺好，就是简单来说，深度学习中的正则化方法就是“通过把一部分不重复的复杂信息损失掉，以此来降低拟合难度以及过拟合的风险，从而加速了模型的收敛”，Normalization目的就是为了让分布稳定下来（降低各维度数据的方差）。所以我们选择不同的Normalization方法，就是针对问题选择在对应维度上进行损失信息。

而对于NLP任务中，同一batch之间的样本（即句子或者句子对之间）关联比较重要，本身我们就是为了通过大量样本对比学习句子中的语义结构，所以做batch Normalization效果不是很好，选择Layer Normalization对样本内部进行损失信息，反而能降低方差。在论文：Rethinking Batch Normalization in Transformers中，作者对于Transformer中BN表现不好的原因做了一定的empirical和theoretical的分析，其中主要问题是在前向传播和反向传播中，batch统计量和其贡献的梯度都会呈现一定的不稳定性（如下图，在使用BN的Transformer训练过程中，每个batch的均值与方差一直震荡，偏离全局的running statistics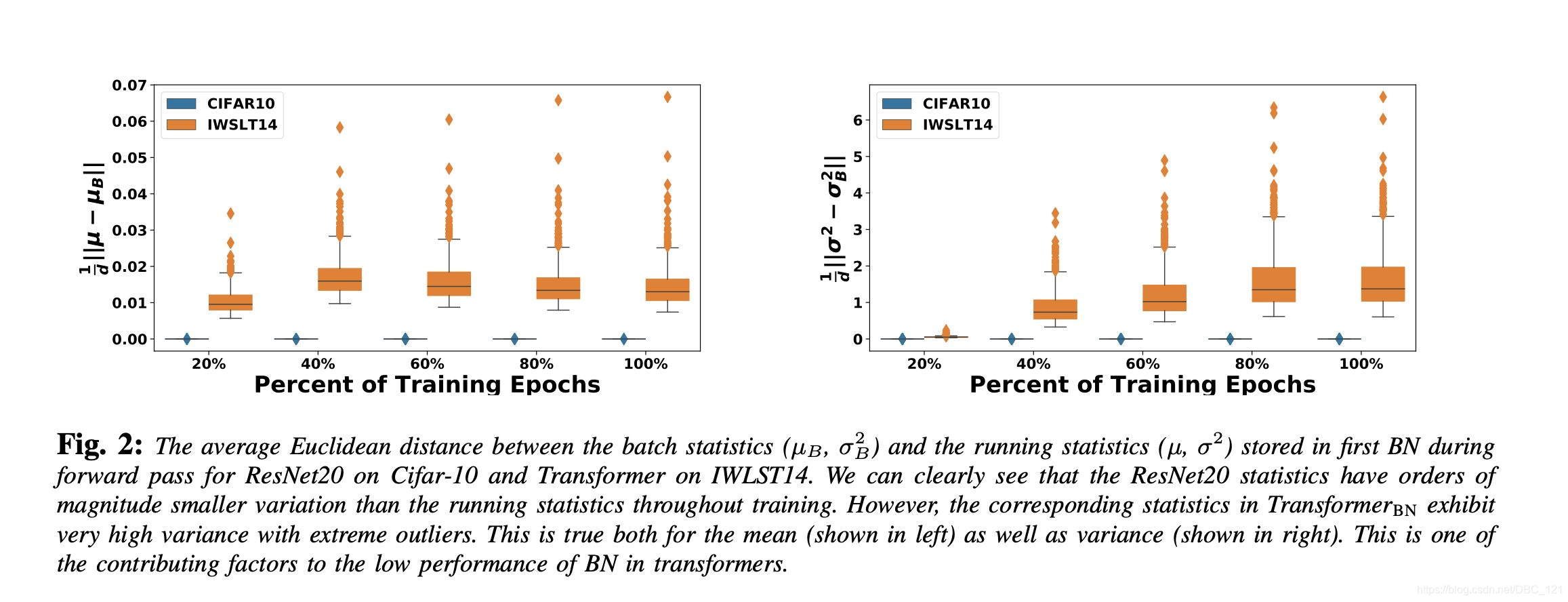）在这里插入图片描述

选择什么样的归一化方法，取决于你关注数据的那部分信息，如果某个维度信息的差异性很重要，需要被拟合，那就别在那个维度上进心Normalization。