前言

标题：Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
原文链接：Link
Github：NLP相关Paper笔记和代码复现
说明：阅读论文时进行相关思想、结构、优缺点，内容进行提炼和记录，论文和相关引用会标明出处，引用之处如有侵权，烦请告知删除。
转载请注明：DengBoCong

在很多实际应用问题中，我们需要对长序列时间序列进行预测，例如用电使用规划。长序列时间序列预测（LSTF）要求模型具有很高的预测能力，即能够有效地捕捉输出和输入之间精确的长程相关性耦合。最近的研究表明，Transformer具有提高预测能力的潜力，但是Transformer存在一些严重的问题，如二次时间复杂度、高内存使用率以及encoder-decoder体系结构的固有限制。为了解决这些问题，本篇论文设计了一个有效的基于Transformer的LSTF模型，即Informer，它具有如下三个显著的特点：

ProbSparse Self-Attention，在时间复杂度和内存使用率上达到了 $O(LlogL)$，在序列的依赖对齐上具有相当的性能。
self-attention 提取通过将级联层输入减半来突出控制注意，并有效地处理超长的输入序列。
产生式decoder虽然概念上简单，但在一个正向操作中预测长时间序列，而不是一步一步地进行，这大大提高了长序列预测的推理速度。

在四个大规模数据集上的大量实验表明，Informer的性能明显优于现有的方法，为LSTF问题提供了一种新的解决方案。

背景介绍

在开始之前，先来感受一下LSTM在长序列中的一个例子的实验结果：

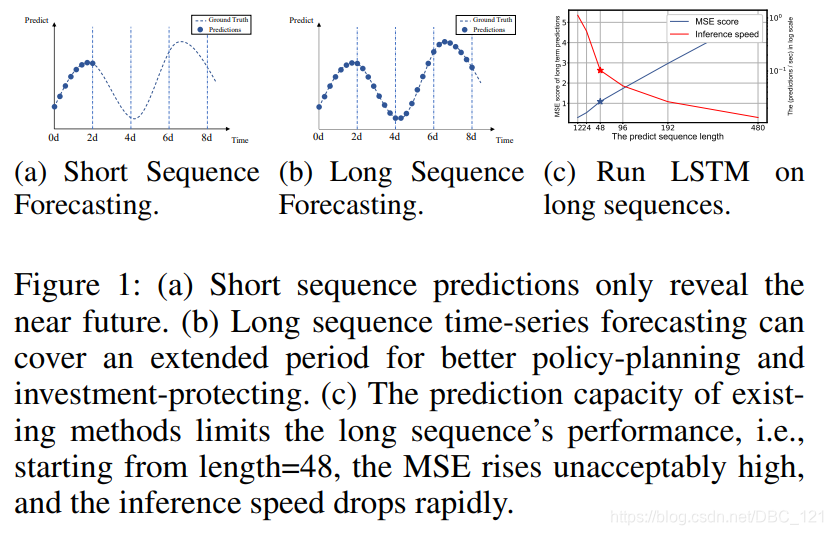
随着数据量的增加，很明显LSTF的主要挑战是增强预测能力以满足日益增长的序列需求，即要求模型具有

出色的long-range对齐能力
对长序列输入和输出的有效操作

Transformer的出现，由于其自注意力机制可以减少网络信号传播路径的最大长度至理论最短 $O(1)$，从而是Transformer表现出了解决LSTF问题的巨大潜力。但是，自注意力机制的计算、内存和架构效率也成为了Transformer应用解决LSTF问题的瓶颈，因此，本论文研究Transformer是否可以提高计算、内存和架构效率，以及保持更高的预测能力？

首先得了解，原始Transformer应用在LSTF上的效率限制问题：

self-attention的二次计算复杂度，self-attention机制的操作，会导致我们模型的时间复杂度为 $O(L^2)$
长输入的stacking层的内存瓶颈：$J$ 个encoder/decoder的stack会导致内存的使用为 $O(J*L^2)$
预测长输出的速度骤降：动态的decoding会导致step-by-step的inference非常慢

论文中提到了许多Transformer的改进版本，如Sparse Transformer、LogSparse、Transformer、LongFormer、reformer、Linformer、Transformer-XL、Compressive Transformer等等，不过都只是局限于解决上述第一个问题，而本文提出的Informer方案同时解决了上面的三个问题，论文中研究了在self-attention机制中的稀疏性问题，本文的贡献有如下几点：

提出Informer来成功地提高LSTF问题的预测能力，这验证了类Transformer模型的潜在价值，以捕捉长序列时间序列输出和输入之间的单个的长期依赖性；
提出了ProbSparse self-attention机制来高效的替换常规的self-attention并且获得了 $O(LlogL)$ 的时间复杂度以及 $O(LlogL)$ 的内存使用率；
提出了self-attention distilling操作，它大幅降低了所需的总空间复杂度 $O((2-\epsilon)LlogL)$
提出了生成式的Decoder来获取长序列的输出，这只需要一部，避免了在inference阶段的累积误差传播

问题定义

在开始介绍具体细节之前，需要先给出问题的定义，在固定大小的窗口下的rolling forecasting（滚动式预测是一种随时间流逝而进行的推测）中，我们在时刻 $t$ 的输入为 $X^t={x_1^t,x_2^t,…,x_{L_z}^t|x_i^t\in R^{d_x}}$ ，我们需要预测对应的输出序列 $Y^t={y_1^t,y_2^t,…,y_{L_y}^t|y_i^t\in R^{d_y}}$，LSTF问题鼓励输出一个更长的输出，特征维度不再依赖于univariate case（$d_y\geq1$）

Encoder-decoder结构：许多流行的模型被设计对输入表示 $X^t$ 进行编码，将 $X^t$ 编码为一个隐藏状态表示 $H^t={h_1^t,…,h_{L_h}^t}$，并且将输出的表示 $Y^t$ 解码，在推断的过程中，通过step-by-step的过程（dynamic decoding），即decoder从前一个状态 $h_k^t$ 计算一个新的隐藏状态 $h_{k+1}^t$ 以及第 $k$ 步的输出，然后对 $k+1$ 个序列进行预测 $y_{k+1}^t$

输入表示：为增强时间序列输入的全局位置上下文和局部时间上下文，给出了统一的输入表示，如下（更详细符号意义可参见原文附录B）：
$$\chi_{feed[i]}^t=\alpha u_i^t+PE_{(L_x\times (t-1)+i,)}+\sum_p[SE_{(L_x\times (t-1)+i)}]_p$$
其中，$\alpha$是在标量投影和局部投影之间平衡大小的因子，如果输入序列已经标准化过了，则推荐值为1，下图是输入表示的直观的概述：
在这里插入图片描述

模型方法细节

现有的时序方法预测大致分为两类：1)：经典的时间序列模型；2):RNN及其变体为代表的encoder-decoder结构的深度学习模型。Informer模型基于encoder-decoder结构，目标是解决LSTF问题，其模型结构概览图如下：
在这里插入图片描述

高效的Self-attention机制

传统的self-attention输入为(query,key,value)，表示为：$A(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d}})$，其中 $Q\in R^{L_Qd}$，$K\in R^{L_Kd}$，$V\in R^{L_V*d}$，$d$ 是输入维度，第 $i$ 个attention被定义为kernel 平滑的概率形式：
$$A(q_i,K,V)=\sum_j\frac{k(q_i,k_j)}{\sum_lk(1_i,k_l)}v_j=E_{p(k_j|q_i)}[v_j]\tag{1}$$
self-attention需要 $O(L_QL_K)$ 的内存以及二次的点积计算代价，这是预测能力的主要缺点。先前的一些研究表明，自注意概率的分布具有潜在的稀疏性，所以在这些研究中，已经针对所有 $p(k_j|q_i)$ 设计了一些“选择性”计数策略。但是，这些方法仅限于采用启发式方法进行理论分析，并使用相同的策略来解决多头自注意的问题，这也缩小了进一步改进的范围。

在论文中，首先对典型自注意的学习注意模式进行定性评估。“稀疏性” self-attention得分形成长尾分布，即少数点积对主要注意有贡献，其他点积对可以忽略。论文使用原始Transformer在ETTH数据集研究self-attention的特征图分布，如下图（选用Layer1中的Head1和Head7的分数）：
在这里插入图片描述

那么，下一个问题是如何区分它们？

Query Sparsity评估

在上一小节的公式（1）中，第 $i$ 个查询对所有key的关注度定义为概率 $p(k_j|q_i)$，我们定义第 $i$ 个query sparsity评估为：
$$M(q_i,K)=ln\sum_{j=1}^{L_k}e^{\frac{q_ik_j^T}{\sqrt{d}}}-\frac{1}{L_K}\sum_{j=1}^{L_K}\frac{q_ik_j^T}{\sqrt{d}}$$
其中，第一项 $q_i$ 是在所有key的Log-Sum-Exp(LSE)，第二项是arithmetic均值。

ProbSparse Self-attention：
$$A(Q,K,V)=Softmax(\frac{\bar{Q}K^T}{\sqrt{d}})V$$
其中 $\bar{Q}$ 是和 $q$ 相同大小的稀疏矩阵，它仅包含稀疏评估下 $M(q,M)$ 下Top-u的queries，由采样factor $c$ 所控制，我们令$u=c\cdot lnL_Q$，这么做self-attention对于每个query-key lookup就只需要计算 $O(lnL_Q)$ 的内积，内存的使用包含$O(L_KlnL_Q)$，但是我们计算的时候需要计算每对的dot-product，即 $O(L_QL_K)$，同时LSE还会带来潜在的数值问题，受此影响，本文提出了query sparsity 评估的近似，即：
$$\bar{M}(q_i,K)=\underset{j}{max}{\frac{q_ik_j^T}{\sqrt{d}}}-\frac{1}{L_K}\sum_{j=1}^{L_K}\frac{q_ik_j^T}{\sqrt{d}}$$
具体证明将附录D，下图是直观的数值性示例：

在实践中，查询和键的输入长度通常是相等的，即 $L_Q = L_K = L$，这么做可以将时间和空间复杂度控制到$O(LlnL)$

Encoder：允许在内存使用限制下处理更长的顺序输入

Encoder设计用于提取长序列输入的鲁棒的 long-range相关性，在前面的讨论我们知道，在输入表示之后，第 $t$ 个序列输入 $X^t$ 已表示为矩阵 $X_{feed_en}^t\in\mathbb{R}^{L_x\times d_{model}}$，下面是Encoder的示意图：
在这里插入图片描述

Self-attention Distilling

作为ProbSparse Self-attention的自然结果，encoder的特征映射会带来 $V$ 值的冗余组合，利用distilling对具有支配特征的优势特征进行特权化，并在下一层生成focus self-attention特征映射。它对输入的时间维度进行了锐利的修剪，如上图所示，$n$ 个头部权重矩阵（重叠的红色方块）。受扩展卷积的启发，我们的“distilling”过程从第 $j$ 层往 $j+1$ 推进：
$$X_{j+1}^t=MaxPoll(ELU(Conv1d([X_j^t]{AB})))$$
其中 $[\cdot]{AB}$ 包含Multi-Head ProbSparse self-attention以及重要的attention block的操作。为了增强distilling操作的鲁棒性，我们构建了halving replicas，并通过一次删除一层（如上图）来逐步减少自关注提取层的数量，从而使它们的输出维度对齐。因此，我们将所有堆栈的输出串联起来，并得到encoder的最终隐藏表示。

Decoder：通过一个正向过程生成长序列输出

此处使用标准的decoder结构，由2个一样的multihead attention层，但是，生成式inference被用来缓解速度瓶颈，我们使用下面的向量喂入decoder：
$$X_{feed_de}^t=Concat(X_{token}^t,X_0^t)\in \mathbb{R}^{(L_{token}+L_y)\times d_{model}}$$
其中，$X_{token}^t\in \mathbb{R}^{(L_{token}+L_y)\times d_{model}}$是start token，$X_0^t\in\mathbb{R}^{L_y\times d_{model}}$ 是一个placeholder，将Masked multi-head attention应用于ProbSparse self-attention，将mask的点积设置为 $-\infty$。它可以防止每个位置都关注未来的位置，从而避免了自回归。一个完全连接的层获得最终的输出，它的超大小取决于我们是在执行单变量预测还是在执行多变量预测。

Generative Inference

我们从长序列中采样一个 $L_{token}$，这是在输出序列之前的slice。以图中预测168个点为例（7天温度预测），我们将目标序列已知的前5天的值作为“start token”，并将 $X_{feed_de}={X_{5d},X_0}$ 输入生成式推断Decoder。$X_0$ 包含目标序列的时间戳，即目标周的上下文。注意，我们提出的decoder通过一个前向过程预测所有输出，并且不存在耗时的“dynamic decoding”。

选用MSE 损失函数作为最终的Loss。

实验结果

看实验结果之前，我们先来看看实验的模型组件的详细信息：
ProbSparse self-attention实现伪代码
超参微调范围：
各个模型在ETT数据集上的实验对比
实验效果如下，从中我们可以发现论文所提出的模型Informer极大地提高了所有数据集的推理效果（最后一列的获胜计数），并且在不断增长的预测范围内，它们的预测误差平稳而缓慢地上升。同时，query sparsity假设在很多数据集上是成立的，Informer在很多数据集上远好于LSTM和ERNN。
参数敏感性实验如下，从下图中，我们发现：（1）Input Length中，当预测短序列（如48）时，最初增加编码器/解码器的输入长度会降低性能，但进一步增加会导致MSE下降，因为它会带来重复的短期模式。然而，在预测中，输入时间越长，平均误差越低：信息者的参数敏感性。长序列（如168）。因为较长的编码器输入可能包含更多的依赖项。（2）Sampling Factor中，我们验证了冗余点积的查询稀疏性假设，实践中，我们把sample factor设置为5即可，即 $c=5$ 。（3）Number of Layer Stacking中，Longer stack对输入更敏感，部分原因是接收到的长期信息较多
解耦实验：从下表中我们发现，（1）ProbSparse self-attention机制的效果：ProbSparse self-attention的效果更好，而且可以节省很多内存消耗（2）self-attention distilling：是值得使用的，尤其是对长序列进行预测的时候（3）generative stype decoderL：它证明了decoder能够捕获任意输出之间的长依赖关系，避免了误差的积累；
计算高效性：（1）在训练阶段，在基于Transformer的方法中，Informer获得了最佳的训练效率。（2）在测试阶段，我们的方法比其他生成式decoder方法要快得多。